Eine Zeitkapsel ist ein Behälter zur Aufbewahrung von Dingen, der erst nach Ablauf eines bestimmten Zeitintervalls von Personen geöffnet wird oder werden darf, mit dem Zweck, zeittypische Dinge für nachfolgende Generationen zu bewahren und zu dokumentieren.1
Einführung
Die Petition 24892 mit dem Titel „Mise en place d'une commission d'enquête pluridisciplinaire indépendante censée conclure sur la réalité sanitaire, statistique, scientifique et politique pour la période Covid-19 au Luxembourg“ wurde im Oktober 2022 eingereicht, als zulässig bewertet, und war ab dem 17. Januar 2023 für Unterschriften freigegeben. Nach 6 Wochen hatten sich am 10. März 4848 Unterzeichner gefunden und die notwendige Schwelle war somit erreicht. Nachdem das Datum bereits zweimal verlegt worden war, sollte am 19. Juli die Anhörung im Parlament erfolgen. Diese wurde jedoch kurzfristig auf ein noch festzulegendes Datum nach den Parlamentswahlen vom 8. Oktober verlegt. Insgesamt wird also vom Zeitpunkt der Einreichung bis zur öffentlichen Debatte mindestens ein ganzes Jahr vergehen.
Eine am 23. März 2023 von der ADR eingereichte Resolution 4108 mit dem Titel „Analyse de la gestion de la pandémie Covid par une commission d'enquête indépendante“ wurde von der Mehrheit der Parlamentarier abgelehnt, einzig die ADR und „déi Lénk“ stimmten dafür3.
Eine Aufarbeitung der in den Jahren 2020 bis 2022 im Zusammenhang mit der Pandemie stehenden sanitären Massnahmen ist offensichtlich nicht erwünscht. Die Frage welche unabhängigen Experten schlussendlich diesen Untersuchungsausschuss bilden sollen, möchten wir erst gar nicht stellen: welcher Wissenschaftler oder Mediziner in Luxemburg war nicht involviert und wäre somit genötigt sich selbst ein Urteil ohne Interessenkonflikte auszustellen?
Auch scheint der Wille nach Aufarbeitung bei der überwiegenden Mehrheit der Bevölkerung zumindest zur Zeit nicht erwünscht zu sein. Man ist „froh dass es vorbei ist“ und möchte bestenfalls nicht mehr daran erinnert werden. Vielleicht möchte man diese traumatische Zeit auch einfach nur verdrängen und hoffen, dass sie sich nicht wiederholt.
Im Sommer 2023 wo diese Zeilen geschrieben werden, haben sich die Indizien mittlerweile verdichtet und legen nahe, dass die Realität sich wesentlich vom offiziellen Narrativ eines neuen, gefährlichen Virus, welcher nur durch eine experimentelle „sichere und effiziente Impfung“ bezwungen werden kann, unterscheidet: Laborursprung des Virus4, Gain-of-Function-Forschung5, methodische Fehler bei den offiziellen Zulassungsstudien der Covid19-Impfstoffe6, durch FOIA freigeklagte Dokumente welche 75 Jahre unter Verschluss bleiben sollten7, geleakte Twitter-8, Lockdown-Files9 und EMA-Dokumente10, Auswertung von Pharmakovigilanz-11 und Krankenkassen-Daten12 in Bezug auf Impfschäden, Nachweis von Plasmiden und DNA in den Impfstoffen13, pathologische Untersuchungen an nach Impfung Verstorbenen14, nachgewiesene systematische Schädlichkeit der mRNA-Technologie15, um nur einige zu nennen.
Wir glauben nicht, dass die Zeit für eine Aufarbeitung bereits gekommen ist. Diese ist jedoch unumgänglich, damit begangene Fehler erkannt werden und sich in Zukunft nicht wiederholen. Genauso wie vieles dafür spricht, dass die Corona-Krise nicht einfach so aus dem Nichts entstand, sondern als eine logische Konsequenz aus vorhergehenden Ereignissen gesehen werden kann16, so wird vermutlich auch die nächste Pandemie nicht lange auf sich warten lassen, da es auch hierfür aktuelle Indizien gibt.
Wir sehen diese Serie an Beiträgen daher eher als eine Art Zeitkapsel, die vielleicht irgendwann eine Bedeutung bekommt, wenn die Zeit reif ist. Somit empfinden wir dies für uns persönlich dann auch als eine Art Ritual dieses Thema abzuschließen. Parallel möchten wir trotzdem die Kandidaten der Parlaments-Wahlen 2023 auffordern, zu den hier getätigten Überlegungen Stellung zu beziehen.
In der Corona-Pandemie wurde viel mit Zahlen gearbeitet: tägliche Fallzahlen/Neuinfektionen, Krankenhausaufenthalte, Reproduktionszahl, Inzidenzraten, Impfstoff-Effektivität und dergleichen mehr. Wir beschränken uns in dieser Artikelserie auf die Analyse dieser Daten und untersuchen, auf welche Art und Weise sie interpretiert wurden.
Viele Artikel zu diesen Themen wurde auf Expressis Verbis bereits veröffentlicht. Mit einem zeitlichen Abstand betrachtet, werden allerdings Zusammenhänge sichtbar, die damals nur erahnt werden konnten. Teilweise wurden Analysen noch vertieft und erweitert, teilweise wurden Themen didaktisch besser aufgearbeitet. Auch neue „Erkenntnisse“ werden vorgestellt.
Lockdown revisited
Im März 2020 war der offizielle „Stand der Wissenschaft“ zu SARS-CoV-2 folgender: es handele sich um ein neues Virus, welches auf eine „immun-naive“ Bevölkerung traf, die also keinerlei Immunabwehr dagegen hatte: folglich würde es sich ungebremst exponentiell ausbreiten und das Gesundheitssystem überlasten. Einziger Ausweg wäre „flatten the curve“ durch Lockdown. Was ohne entsprechende Maßnahmen sich zutragen würde, hatte der Epidemiologe Ferguson vom Imperial College of London mittels mathematischen Modellen ausgerechnet: die Apokalypse schlechthin mit überlasteten Krankenhäusern und unzähligen Toten17. Dass er mit ähnlichen Berechnungen bei der Schweinegrippe 2009 schon um Größenordnungen daneben lag18, und ausserdem durch Spenden von der Pharmaindustrie nahestehenden Stiftungen in Interessenkonflikte verwickelt war19, interessierte damals offenbar niemanden, auch die luxemburgische Wissenschaftsgemeinde nicht.
In dem Schlüsseldokument „Policy brief: Beitrag der luxemburgischen Forschung zu Luxemburgs EXIT-Strategie im Rahmen der COVID-19 Pandemie“ welches Anfang Mai 2020 Research Luxembourg herausgab um die Regierung in ihrer Covid-Politik zu beraten, lesen wir gleich zu Beginn20:
Weltweit wurden restriktive Maßnahmen von Regierungen getroffen, immer mit dem Ziel, die exponentielle Vermehrung des neuartigen Coronavirus zu bremsen, damit die Gesundheitssysteme des jeweiligen Landes nicht kollabieren. So auch in Luxemburg. Auf die COVID-19 Pandemie hat Luxemburg bisher sehr gut reagiert. Aufgrund des Lockdowns, der entschieden eingeführt und gut von der Bevölkerung umgesetzt wurde, ist es Stand heute unwahrscheinlich, dass es zu einem Kollaps des luxemburgischen Gesundheitssystems kommen wird – unter der Voraussetzung, dass die restriktiven Maßnahmen nicht zu schnell aufgehoben werden.
Es wird eine Grafik gezeigt, welche die verschieden Szenarien zeigt: mit und ohne Lockdown.
Wir wollen uns mit der grauen Kurve beschäftigen, welche den Verlauf der kumulativen positiven Fälle zeigt,falls kein Lockdown stattgefunden hätte: das „No lockdown“ scenario. Insbesondere möchten wir herausfinden, ob dieses postulierte Wachstum kohärent mit anderen in diesem Zusammenhang beobachteten Größen ist.
Dazu müssen wir uns zunächst mit 2 Dingen beschäftigen:
einigen Grundeigenschaften exponentiellen Wachstums21
dem Zeitabstand zwischen einer Infektion und dem Eingehen dieser als positiver PCR-Test in die Statistik
Grundeigenschaften exponentiellen Wachstums
Für das weitere Verständnis brauchen wir etwas Hintergrundwissen, welches nicht kompliziert ist, in der hier dargebotenen Zusammenstellung jedoch im Allgemeinen nicht vermittelt wird.
Damit es anschaulich bleibt, betrachten wir zunächst ein einfaches Beispiel exponentiellen Wachstums: ein Sparschwein, in das wir jeden Tag die gleiche Geldsumme hineinwerfen, die sich bereits darin befindet.
Die erste Zeile der folgenden Tabelle zeigt das betrachtete Zeitintervall:
die Tage 0 bis 7.
In der zweiten Reihe steht die Geldsumme, welche sich an dem entsprechenden Tag im Sparschwein befindet, auch noch kumulative Summe genannt. Diese setzen wir für den Tag 0 gleich eins.
Die dritte Reihe gibt für jeden Tag an, welche Geldsumme wir in das Sparschwein werfen müssen, also der tägliche Zuwachs (diese ist gleich der kumulativen Summe des Vortages).
Am Tag 1 werfen wir 1 Euro in das Sparschwein, welches dem Betrag in Zeile „Summe“ am Vortag (Tag 0) entspricht, die kumulative Summe erhöht sich auf
1 + 1 = 2.Am Tag 2 werfen wir 2 Euro in das Sparschwein, welches dem Betrag in Zeile „Summe“ am Vortag (Tag 1) entspricht, die kumulative Summe erhöht sich auf
2 + 2 = 4.
Wir wiederholen diese Schritte bis zum 7. Tag und erhalten folgende in der Tabelle angezeigten Werte:
Wir haben uns bis jetzt noch nicht mit der letzten Spalte beschäftigt: hier wird der Inhalt jeder Zeile mathematisch beschrieben.
In der ersten Zeile steht die Variable, die wir für die einzelnen Tage benutzen: t
In der zweiten Reihe schreiben wir die kumulative Summe oder Wachstumsfunktion als Funktion f der Zeit t also f(t). Diese ist, wie man leicht sieht, gleich der Potenzen von 2:
Wir erhalten also aufeinanderfolgend die Werte:
Der tägliche Zuwachs am Tage t bezeichnen wir mit Δf(t). Er berechnet sich aus der Differenz der Wachstumsfunktion an den Tagen t und t - 1 :
Beispiel für t = 4 :
Die Werte entsprechen denen der Summe, allerdings um einen Tag nach hinten verschoben.
Wir erhalten die Eigenschaft 1: der tägliche Zuwachs eines exponentiellen Wachstums ist selbst auch wieder exponentiell.
Wir kommen nun zur 4. Reihe: hier betrachten wir die Wachstumsrate r(t). Diese ergibt sich bekannterweise für den Tag t, wenn wir den Quotienten aus Zuwachs am Tage t und Wachstumsfunktion am Vortag t - 1 bilden:
Wenn wir die Wachstumsrate für einen beliebigen Tag rechnen, so fällt auf, dass diese immer gleich ist:
Wir erhalten die Eigenschaft 2: die Wachstumsrate eines exponentiellen Wachstums ist konstant.
Schließlich betrachten wir in Zeile 5 noch die effektive Reproduktionszahl, welche bekanntermaßen angibt, wieviele Personen ein Infizierter durchschnittlich ansteckt. Man benötigt zu dieser Berechnung das sogenannte serielle Intervall22, welches vereinfacht ausgedrückt in einer Infektionskette den durchschnittlichen zeitlichen Abstand von Infektion bis zur Weitergabe des Krankheitserregers (Infizierung) angibt. Für das SARS-CoV-2-Virus übernehmen wir von Research Luxembourg einen Wert von 4 Tagen. Die effektive Reproduktionszahl Reff(t) am Tage t berechnet sich dann nach der Formel:
Wenn wir wieder die effektive Reproduktionszahl für einen beliebigen Tag rechnen, so erhalten wir ein ähnliches Resultat wie für die Wachstumsrate:
Wir erhalten die Eigenschaft 3: die effektive Reproduktionszahl eines exponentiellen Wachstums ist konstant.
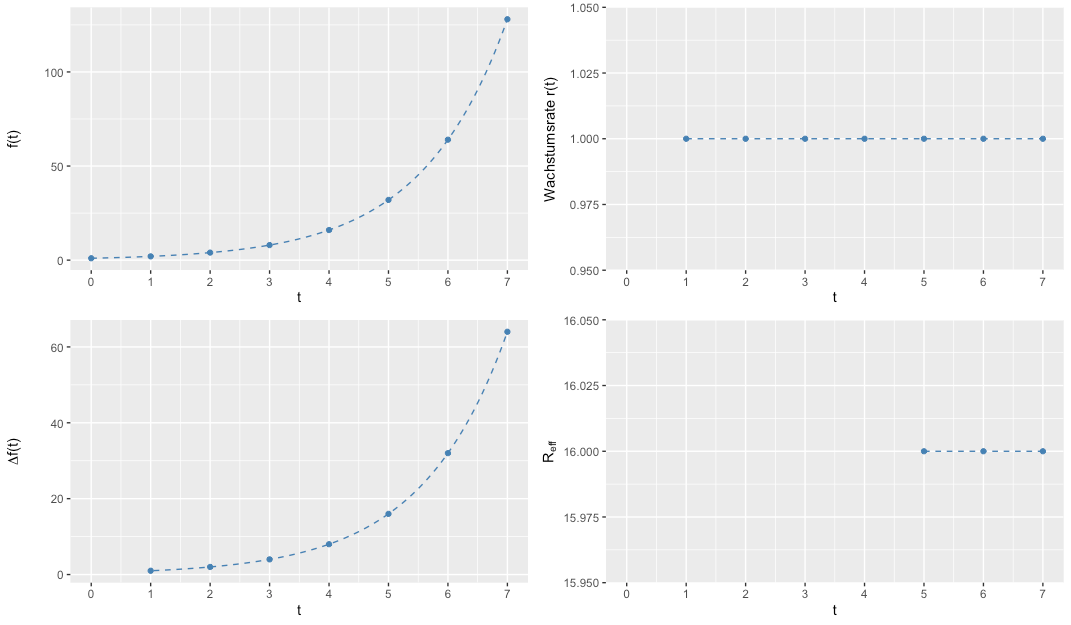
Wachstumsfunktion, täglicher Zuwachs, Wachstumsrate und effektive Reproduktionszahl sind nachfolgend noch einmal grafisch dargestellt.
Zeitabstand zwischen Infektion und Eingang in die Statistik
Das Grundprinzip von Ursache und Wirkung besagt, dass die Ursache zeitlich immer vor der Wirkung eintreten muss. Möchten wir die Wirkung des Lockdowns auf die Entwicklung der Infektionen einschätzen, müssen wir also zunächst alle in diesem Zusammenhang beteiligten Ereignisse auf der Zeitachse richtig anordnen.
Die in Abbildung 1 gezeigte Wachstumsfunktion / kumulative Summe der positiven „Fälle“ / PCR-Tests zeigt für ein entsprechendes Datum auf der horizontalen X-Achse nicht die Summe der sich bis zu diesem Zeitpunkt ereigneten Neuinfektionen, sondern die Summe derjenigen, die bis dato statistisch registriert wurden.
Research Luxembourg hatte auf der Platform GitHub den Quellcode des Python-Programmes publiziert, mit dem sie die effektive Reproduktionszahl ausgerechnet haben23. In diesem sehr wichtigen Dokument, auf das wir noch zurückkommen werden, finden wir den Hinweis:
Note: during COVID-19 pandemics, there is a delay from infection to detection during to latency, sampling times and so on. Hence, it is necessary to refer all data to their true infection time. Here, we assume constant shift. By comparison with more advanced nowcasting procedures (e.g. RKI's), we estimated such shift to be equal 8±1 days. Hence, be aware that we are looking at the past. This is considered in plots below.
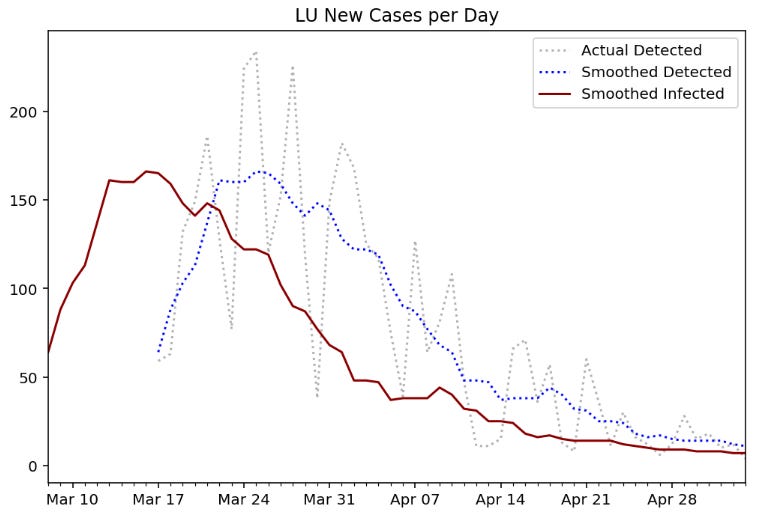
Wir gehen also von einer Zeitverzögerung von 8±1 Tagen aus, mit der eine Infektion in der Statistik erfasst wird. Bei den auf GitHub gezeigten Grafiken werden die Kurven von Infektion und Eingang in Statistik mit „infected“ beziehungsweise „detected“ bezeichnet. Hierzu ein Beispiel:
Es ist zu bemerken, dass dieser Tatbestand nicht immer konsequent erwähnt und bei der Auswertung davon betroffener Zeitreihen somit auch nicht immer berücksichtigt wird.
Möchte man Ereignisse relativ zueinander auf der Zeitachse korrekt anordnen, gibt es prinzipiell 2 Möglichkeiten:
Wie eben gezeigt, durch zeitliches Verschieben nach vorne der statistischen Daten der Infektionen um 8 Tage.
Durch Berücksichtigung der Tatsache, dass jedes andere Ereignis auf der Zeitachse, das nicht dieser Latenz von 8 Tagen unterliegt (zB. jede Art von Nonpharmaceutical Intervention - NPI), erst nach dieser Zeitspanne eine Wirkung zeigen kann.
Wir entscheiden uns für die zweite Option.
Vergleich „No Lockdown“-Szenario mit realen Daten
Wir haben nun alle Elemente zusammen, um die Analyse durchführen zu können. Als erstes „bauen“ wir das „No Lockdown“-Szenario in Abbildung 1 als exakte Funktion nach - wir müssen also die entsprechende Gleichung aufstellen. Die hierzu benötigte Information steht teilweise in der Grafik: es wird eine Verdopplungszeit von 2,28 Tagen angegeben ( τ2PI= 2,28 d ). Für die entsprechende Exponentialfunktion, welche wir mit E(t) bezeichnen möchten, folgt daraus:
Die detaillierten Rechnungen finden sich im Anhang. Bleibt noch der Faktor k zu bestimmen. Nehmen wir den 29. Februar, der Tag als zum ersten Mal eine Person positiv getestet wurde, als t = 0, dann ergibt ein visueller Abgleich für k einen Wert von 1. Somit erhalten wir für E(t):
Für den täglichen Zuwachs, die Wachstumsrate und die effektive Reproduktionszahl erhalten wir jeweils:
In der folgenden Abbildung sind nun die 4 Funktionen dargestellt.
Die linke obere Grafik zeigt die „nachgebaute“ Abbildung 1. Die schwarzen Punkte sind die realen Daten, wie sie beispielsweise auf https://covid19.public.lu/fr/graph.html veröffentlicht sind. Die blaue Kurve ist die exponentielle Funktion E(t). Die angesprochene Zeitverzögerung zwischen Infektion und Eingang in die Statistik ist durch den dunkelgrauen Bereich gekennzeichnet: er beginnt mit dem Lockdown am 16. März 2020 und endet 8 Tage später. Einen Einfluss auf das Infektionsgeschehen kann sich also frühestens danach manifestieren, oder anders ausgedrückt: bis zum 24. März müsste sich das postulierte exponentielle Wachstum ungebremst fortsetzen. Wir sehen hier bereits, dass E(t) und realer Verlauf gegen Ende auseinander driften.
Links unten ist der tägliche Zuwachs dargestellt. Die schwarzen Punkte sind wieder die realen Daten, also die Anzahl positiver PCR-Tests pro Tag. Der gleitende Mittelwert über 7 Tage ist als gestrichelte Linie zusätzlich eingezeichnet, er erlaubt ein klareres Bild des zeitlichen Verlaufs dieser Größe, welche doch starken Schwankungen unterliegt. Die blaue Kurve ist jetzt der von E(t) abgeleitete tägliche Zuwachs Δf(t), welcher ja wiederum exponentiell ist. Wir sehen hier noch klarer, dass der vorhergesagte Verlauf wesentlich von den realen Daten abweicht: Δf(t) ist als Exponentialfunktion stets konvex, während offensichtlich der Graph des Mittelwertes der täglichen Fallzahlen für den betreffenden Zeitraum konkav ist.
Das Bild rechts oben zeigt die Wachstumsrate, wobei die aus E(t) berechnete konstante Funktion wiederum in blau dargestellt ist. Die entsprechenden Werte für die realen Daten erhalten wir dadurch, dass wir für einen Tag t den täglichen Zuwachs durch die kumulative Summe am Vortag t - 1 teilen. Der gleitende Mittelwert wurde wieder gestrichelt hinzugefügt. Die Werte schwanken anfangs sehr stark, da die Anzahl täglicher positiver PCR-Test zu diesem Zeitpunk noch sehr klein ist. Wir haben die vertikale y-Achse logarithmisch skaliert: zum einen, weil die Werte für die Wachstumsrate einen sehr weiten Bereich umspannen, und zum anderen, weil auf diese Weise auch offensichtlich wird, dass diese Größe einen exponentiellen Abfall beschreibt (fallende Gerade bei logarithmischer Skalierung der y-Achse). Auch hier wird wieder die Diskrepanz zwischen exponentiellen Wachstum und Realität sichtbar.
Die letzte Grafik zeigt schließlich die effektive Reproduktionszahl, einmal als von der exponentiellen Wachstumsfunktion abgeleiteten konstanten Funktion in blau, einmal als die wie im Mai 2020 von Research Luxembourg berechnete. Hierzu wurden die Daten vom 13. Mai 2020 der Webseite https://msan.gouvernement.lu/de/graphiques-evolution.html benutzt, archiviert auf Wayback Machine unter der URL: https://web.archive.org/web/20200513003917/https://msan.gouvernement.lu/de/graphiques-evolution.html.
Das postulierte exponentielle Wachstum mit einer daraus resultierenden konstanten Reproduktionszahl steht somit im unmittelbaren Widerspruch zu jener von Luxembourg Research selbst berechneten.
In diesem Zusammenhang bietet es sich an, die letzte Grafik des GitHub Dokumentes zu betrachten.
Die obere Grafik zeigt den täglichen Zuwachs an Fällen / positiven PCR-Tests, wobei die rote Kurve gemäß der besprochenen Zeitkorrektur den tatsächlichen Zeitpunkt der Infektion darstellt („smoothed infected“). Die untere Kurve zeigt den entsprechend zeitkorrigierten Verlauf der effektiven Reproduktionszahl, welche von der roten Kurve abgeleitet ist.
Die Reproduktionszahl fällt somit schon ab dem 9. März steil ab, was als unwiderlegbarer Beweis gelten kann, dass Research Luxembourg sich in vollem Umfang der Tatsache bewusst war, dass das Infektionsgeschehen sich bereits eine Woche vor dem Lockdown verlangsamte.
Wurde die Reproduktionszahl an anderer Stelle publiziert, kam diese Zeitkorrektur jedoch nicht zur Anwendung: in der Statistik von Mai 2020 etwa startet der Abfall entsprechend erst am 16. März, wie der folgende Screenshot der „Wayback machine“ vom 13. Mai 2020 zeigt.
Auf diese Weise kann auf diese Weise natürlich allzu leicht der Eindruck entstehen, die Reproduktionszahl wäre in Folge des Lockdowns gefallen.
Ein alternatives Modell – die Gompertz-Funktion
Ein exponentielles Wachstum wurde in der Folge in der öffentlichen Kommunikation des Gesundheitsministeriums zur permanenten Gefahr deklariert. Es galt, das Virus „an der Gite ze halen“ ( luxemburgischer Ausdruck für “in Schach zu halten”) und jede Unvorsichtigkeit könnte erneut dazu führen, dass „die Zahlen steigen“. Dabei wurde allerdings nie erwähnt, dass ein exponentielles Wachstum nur unter bestimmten Voraussetzungen erfolgen kann: insbesondere ist es dazu notwendig, dass jeder jeden anstecken kann, und somit auch immer genügend „Infizierbare“ im Umfeld der Infektiösen zur Verfügung stehen.
Wir möchten hier ein alternatives Modell vorstellen, zum einen als „Blick über den Tellerrand“, zum anderen auch, weil dieses Modell eine sehr viel tiefergehendes Verständnis der hier betrachteten Wachstumsfunktion erlaubt.
Michael Levitt, Professor an der Stanford University und Nobelpreisträger, zeigte bereits im Mai 2020 in einer Reihe von Online-Videos24, dass die Wachstumsfunktion der Infektionen für die „erste Welle“ mit der sogenannten Gompertz-Funktion auf sehr überzeugende Weise modelliert werden kann. In mehreren wissenschaftlichen Studien wurde dies im Folgenden bestätigt25,26,27. Levitt konnte in einer späteren Arbeit zeigen, dass dieses Verhalten unter bestimmten Annahmen durch Superspreader-Events erklärt werden könnte28.
Benjamin Gompertz (*1779 - †1865) entwickelte 1825 ein Wachstumsmodell für Populationen, indem er die Sterblichkeitsrate eines Individuums mit zunehmenden Alter als exponentiell ansteigend postulierte. Die hieraus abgeleitete Funktion29 ist eine sogenannte Sigmoidfunktion. Man kann leicht nachweisen, dass die Wachstumsrate und Reproduktionszahl dieser Funktion dem Verlauf der beobachteten realen Daten in guter Näherung entsprechen. Wir haben die Parameter diese Funktion mit der „Methode der kleinsten Residuenquadrate“ bestimmt. Das Ergebnis ist in untenstehender Grafik in Pink dargestellt; zum Vergleich wurde das „No Lockdown Scenario“ auch eingezeichnet (in blau). Die Details hierzu finden sich wieder im Anhang.
Wachstumsfunktion, täglicher Zuwachs und Wachstumsrate der realen Daten zeigen offensichtlich eine nicht zu leugnende sehr gute Übereinstimmung mit der Gompertz-Funktion. Für die Reproduktionszahl wurden im Lauf der Zeit von Research Luxembourg verschiedene Versionen publiziert. In der rechts unteren Grafik haben wird die ursprüngliche Berechnung (Mai 2020) in grün und die zuletzt veröffentlichte (2023) in orange eingezeichnet. Auch hier wird das alternative Modell überzeugend bestätigt.
Insbesondere zeigt sich an diesem Modell, dass der Verlauf der Infektionen kontinuierlich bis Ende April beschrieben werden kann, ohne dass einzelne Phasen betrachtet werden müssten. Ein Wechsel im Trend, der sich laut unserer Zeitverzögerung von 8 Tagen ab dem kritischen Zeitpunkt um den 24. März bemerkbar machen müsste, bleibt in allen 4 Graphiken aus. Aus dieser Perspektive betrachtet, läßt sich keinerlei Einfluss des Lockdowns auf die Evolution der Infektionen nachweisen.
Konstruierte Kausalität
Research Luxembourg veröffentlichte im Juli 2020 einen Bericht mit dem Titel: „Analyse der COVID-19 Fallzahlen in Luxemburg im Hinblick auf die derzeitige Lage“30. Auf Seite 2 ist eine upgedatete Version der Abbildung 1 zu sehen. Aus einem sich uns nicht erschließenden Grund sind die Datenpunkte um einen Tag nach vorne verschoben und die Verdopplungszeit ist leicht verschieden. Die Legende sowie ein Ausschnitt, der die Zeit um den Lockdown zeigt, sind nachfolgend abgebildet.
Nebenbei bemerkt: die Bedeutung der hochstellten Buchstaben „PI“ der Verdopplungszeit wird ersichtlich: sie stehen für „Phase I“. Da dieses Bezeichnung auch schon in Abbildung 1 Ende April 2020 benutzt wurde, wusste man somit bereits früh von einem längeren „Kampf“, wo noch etliche andere exponentielle Verläufe nachfolgen sollten...)
Phase II soll einen ersten Effekt des Lockdowns einläuten: „Phase II: First Effect of Lockdown“. Die entsprechende orange Gerade ist ab 19. März durchgezogen. Das „No Lockdown-scenario“ endet also zu diesem Zeitpunkt und einen Tag später sind wir damit schon im linearen Bereich.
Offensichtlich argumentiert man hier so, als würde der dargestellte Verlauf den tatsächlichen Zeitpunkt der Infektionen wiedergeben. Nach der oben besprochenen Zeitkorrektur hat sich dagegen bereits 8 Tage früher, und damit am 11. März, der Anstieg der Anzahl der Neuinfektionen verlangsamt, also zu einem Zeitpunkt, als es bis auf das Absagen größerer Veranstaltungen keinerlei Maßnahmen gab. Wir erinnern uns, dass in diesem Zeitraum (Freitag 13. März) auch die panikartigen Hamsterkäufe in den Supermärkten stattfanden, ohne Maske, Abstand und Plexiglas vor den Kassen und trotzdem kein (erneutes) exponentielles Wachstum auslösen konnten.
Der Beginn der Phase 3 am 28. März soll schließlich als Zeitpunkt verstanden werden, ab dem der Lockdown sein volle Wirkung zeigt („Lockdown delay 12 days“). Um dieses Datum herum wird auch die maximale Anzahl der täglichen Fallzahlen erreicht, zumindest wenn man den in den Medien kommunizierten gleitenden Mittelwert berücksichtigt.
Betrachtet man dagegen, wie im vorherigen Abschnitt bereits erwähnt, den kontinuierlich exponentiellen Abfall der Wachstumsrate, so entpuppt sich diese Zuordnung als rein willkürlich: fällt eine Größe gleichmäßig ab, sind alle Zeitpunkte gleichwertig und keinem kommt eine besondere Bedeutung zu. Die folgende Abbildung illustriert dies: die Phasen 1, 2 und 3 sind jeweils in rot, orange und grün eingefärbt.
Wenn überhaupt, dann hätte sich um den 24. März (Lockdown plus 8 Tage) eine Änderung im Trend bemerkbar machen müssen, was offensichtlich nicht der Fall ist. Insgesamt wird hier also ein zeitlich kausaler Zusammenhang konstruiert, welcher in der Realität so nie existiert hat.
Natürlich kann man argumentieren, dass bereits vor dem Lockdown die Bevölkerung ihr Verhalten angepasst hätte, und auf diese Weise die Wirkung auch entsprechend früher eingesetzt hätte. Dann bleibt allerdings die Frage, mit welchen Parametern man eine solche „Verhaltens-Anpassung“ quantifiziert, und wie man hieraus dann diese Aussage herleitet. Da dies unseres Wissens nach nie erfolgt ist, ist bis auf gegenteiligen Beweis dieses Argument also zurückzuweisen.
Die Darstellung der Wirkung des Lockdowns in den Medien
Tägliche Fallzahlen, mal steigend, mal fallend, sind für die Mehrzahl der Menschen greifbare Informationen, welche zumindest den Eindruck vermitteln, eine Situation realistisch einschätzen zu können. So ist es dann auch wenig verwunderlich, dass genau der Zeitpunkt des Maximums der pro Tag gezählten positiven PCR-Tests am 29. März 2020 (gleitender Mittelwert) als Stichtag für die beginnende Wirkung des Lockdowns auserkoren wurde.
Eine der offiziellen Statistik (s. Abbildung) ähnliche Graphik wurde etwa im Mai 2020 im Luxemburger Wort abgebildet mit der Beschreibung:
Der Verlauf der Kurve der Infektionszahlen (hier der gleitende Mittelwert auf sieben Tage) erklärt sich durch die ungewöhnliche Inkubationszeit von Covid-19 mit im Schnitt zwischen fünf und zehn Tagen. Die Person, die heute zu den Neuinfizierten gezählt wird, hat sich bereits vor Tagen infiziert. Aus diesem Grund hinkt die Statistik der aktuellen Situation hinterher. Nach dem Lockdown und dem Social distancing am 16. März ist zu beobachten, dass die Zahl der täglichen Neuinfektionen rund zwei Wochen später gesunken ist.
Überprüfen wir diese Aussage auf Kausalität mit der Ursache des Lockdowns am 16. und dem Maximum der Neuinfektionen als Wirkung am 29. März 2020.
Zunächst stellen wir fest, dass der gleitende Mittelwert über 7 Tage in der Grafik am letzten Tag ausgewertet wird. Laut dem entsprechenden englischsprachigen Wikipedia-Artikel ist dies im Finanzwesen, jedoch nicht in der Wissenschaft üblich31. Ein geeigneterer Zeitpunkt für das Maximum wäre also der zentrierte Mittelwert, welcher bereits 3 Tage früher am 26. März erreicht wird.
Wir ziehen die 8 Tage Zeitverzögerung zwischen Infektion und Eingang in die Statistik ab und landen beim 18. März.
Betrachtet man beim gleitenden Mittelwert den Zeitraum vor dem Maximum, so erkennt man leicht, dass sich der Anstieg der Neuinfektionen immer mehr verlangsamt, bis er am Maximum ganz zum Erliegen kommt. Dies ist ein natürliches Phänomen, das immer eintritt, wenn die entsprechende Kurve um das Maximum herum „rund“ und nicht „spitz“ verläuft (mathematisch gesprochen: die Ableitung ist zunächst positiv, wird am Maximum Null, und anschließend negativ, wobei sie dabei die ganze Zeit stetig ist). Die Wirkung tritt also bereits früher ein, und das Maximum als Stichtag zu nehmen ist so gesehen wenig sinnvoll: der Wendepunkt (franz.: point d’inflexion) an dem die Zunahme der täglichen Neuinfektionen kleiner wird, wäre also die bessere Wahl. Dieser liegt – vorsichtig geschätzt – mindestens 5 Tage vor dem Maximum, sodass wir wieder eine Wirkung erhalten, welche vor der vermeintlichen Ursache am 16. März angesiedelt ist.
Insgesamt hinkt die Argumentation somit bereits an dieser Stelle. Gravierender ist unserer Meinung nach jedoch, dass man wie selbstverständlich von einer Wirkung des Lockdowns ausgeht, wo dann nur noch zu klären bleibt, wieso diese sich „erst“ nach 2 Wochen bemerkbar gemacht hat. Und selbst wenn die Zahl der täglichen Neuinfektionen später erfolgt wäre, bliebe immer noch zu beweisen, dass der Lockdown und nicht ein anderer Umstand (natürliches Abklingen einer Infektionswelle, Saisonalität des Virus, ...) die Ursache war.
Schlussfolgerungen
1. Der exponentielle Verlauf des postulierten „No Lockdown Scenario“ wird durch die hieraus berechneten Größen „täglicher Zuwachs“ und Wachstumsrate beim Vergleich mit den realen Daten nicht bestätigt, und durch die von Research Luxembourg selbst berechnete Reproduktionszahl sogar widerlegt.
2. Bis zur Erbringung eines gegenteiligen Beweises gilt die Aussage: es gab zu keinem Zeitpunkt ein exponentielles Wachstum. Dies folgt aus der Übereinstimmung der realen Daten mit der Gompertz-Funktion.
3. Durch die mehr oder wenige willkürliche Einteilung in Phasen, sowie durch Ignorieren der Zeitkorrektur werden vermeintliche Effekte des Lockdowns hergeleitet. Auf diese Weise wird eine künstliche Kausalität (Lockdown → Infektionsgeschehen) geschaffen, welche bei einem kontinuierlich exponentiellen Abfall der Wachstumsrate keine mathematische Berechtigung hat.
4. Die Möglichkeit, dass bereits vor dem 16. März eine Verhaltens-Änderung der Bevölkerung eine Auswirkung auf des Infektionsgeschehen hatte, wurde wissenschaftlich nicht bewiesen, und kann daher nicht als Argument benutzt werden.
5. Die Tatsache, dass es kein exponentielles Wachstum gab, und somit auch keines verhindert werden konnte, verlangt nach einer Neubewertung aller nachfolgenden Maßnahmen, also insbesondere dem “Déconfinement“ und dem Large Scale Testing.
6. Insgesamt liegt der Schluss nahe, dass die Bewertung der Wirksamkeit des Lockdowns eine rein politische Funktion zu erfüllen hatte, bei der es ausschließlich um den Erhalt eines Narrativs ging.
Le site des pétitions de la Chambre des Députés: Publique n°2489 - Mise en place d'une commission d'enquête pluridisciplinaire indépendante censée conclure sur la réalité sanitaire, statistique, scientifique et politique pour la période Covid-19 au Luxembourg https://www.petitions.lu/petition/2489
Résolution 4108: Analyse de la gestion de la pandémie Covid par une commission d'enquête indépendante https://www.chd.lu/de/motion_resolution/4108
The Intercept (19.01.2023): EVOLUTION OF A THEORY - Unredacted NIH Emails Show Efforts to Rule Out Lab Origin of Covid
https://theintercept.com/2023/01/19/covid-origin-nih-emails/
The Intercept (09.09.2021): NIH DOCUMENTS PROVIDE NEW EVIDENCE U.S. FUNDED GAIN-OF-FUNCTION RESEARCH IN WUHAN
https://theintercept.com/2021/09/09/covid-origins-gain-of-function-research/
Thacker P D. Covid-19: Researcher blows the whistle on data integrity issues in Pfizer’s vaccine trial BMJ 2021; 375: n2635 doi:10.1136/bmj.n2635 https://www.bmj.com/content/375/bmj.n2635
Public Health and Medical Professionals for Transparency https://phmpt.org/
David Zweig: THE TWITTER FILES: HOW TWITTER RIGGED THE COVID DEBATE
https://twitter.com/davidzweig/status/1607378386338340867
The Telegraph: The Lockdown Files https://www.telegraph.co.uk/news/lockdown-files/
Tinari S. The EMA covid-19 data leak, and what it tells us about mRNA instability BMJ 2021; 372 :n627 doi:10.1136/bmj.n627 https://www.bmj.com/content/372/bmj.n627.long
Open VAERS https://openvaers.com/
Substack - A MIDWESTERN DOCTOR: The Most Important Dataset of the Pandemic Was Just Released
McKernan, Kevin, et al. “Sequencing of Bivalent Moderna and Pfizer Mrna Vaccines Reveals Nanogram to Microgram Quantities of Expression Vector Dsdna Per Dose.” OSF Preprints, 10 Apr. 2023. Web. https://osf.io/b9t7m/
Paul Schreyer: Chronik einer angekündigten Krise
https://www.westendverlag.de/buch/chronik-einer-angekuendigten-krise/
Imperial College COVID-19 Response Team. Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. 2020. https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-NPI-modelling-16-03-2020.pdf
The Guardian (12.05.2009): Swine flu could affect third of world's population, says study https://www.theguardian.com/world/2009/may/12/swine-flu-report-pandemic-predicted
Research Luxembourg (03.05.2020): Policy brief: Beitrag der luxemburgischen Forschung zu Luxemburgs EXIT-Strategie im Rahmen der COVID-19 Pandemie https://www.researchluxembourg.org/wp-content/uploads/2020/05/200507_Proaktive-Einda%CC%88mmungs-Programm_DE.pdf
Research Luxembourg: Daniele Proverbio. Real time Rt estimation. 2020.
Ursprüngliche URL: https://github.com/ResearchLuxembourg/covid-19_reproductionNumber/blob/master/src/estimation_R_eff.ipynb
Backup auf Expressis Verbis:
MHTML-Format: https://www.expressis-verbis.lu/wp-content/uploads/2023/08/res_lux_github_r_t.mhtml_.zip
Screenshot: https://www.expressis-verbis.lu/wp-content/uploads/2023/08/res_lux_github_r_t.png
1. Exponential Growth is Terrifying:
2. Curve Fitting for Understanding:
3. COVID19 Never Grows Exponentially:
Levitt benutzt in den Grafiken den Wachstumsfaktor, dieser steht im Zusammenhang mit der hier besprochenen Wachstumsrate über die Gleichung: Wachstumsfaktor = ln( Wachstumsrate ).
Akira Ohnishi, Yusuke Namekawa und Tokuro Fukui. ”Universality in COVID- 19 spread in view of the Gompertz function“. In: medRxiv (2020). doi: 10.1101/2020.06.18.20135210. https://www.medrxiv.org/content/early/2020/09/05/2020.06.18.20135210
E. Pelinovsky u. a. ”Gompertz model in COVID-19 spreading simulation“. In: Chaos, Solitons & Fractals 154 (2022), S. 111699. issn: 0960-0779.
https://www.sciencedirect.com/science/article/pii/S0960077921010535
Martí Català u.a. ”Empirical model for short-time prediction of COVID-19 spreading“. In: PLOS Computational Biology 16.12 (Dez. 2020), S. 1–18. doi: 10.1371/journal.pcbi.1008431. https://doi.org/10.1371/journal.pcbi.1008431
Zonta F, Scaiewicz A, Levitt M. The Gompertz Growth of COVID-19 Outbreaks is Caused by Super-Spreaders. ArXiv [Preprint]. 2021 Nov 3:arXiv:2111.02962v2. PMID: 34981031; PMCID: PMC8722603. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC8722603/
Gompertz-Funktion: https://de.wikipedia.org/wiki/Gompertz-Funktion
Research Luxembourg (15.07.2020): „Analyse der COVID-19 Fallzahlen in Luxemburg im Hinblick auf die derzeitige Lage https://www.researchluxembourg.org/wp-content/uploads/2020/07/200715_Analysis_COVID-19_15072020_FINAL.pdf